Abstract
This research discusses a new approach, namely two-stage ridge regression analysis, to overcome violations of classical assumptions, especially multicollinearity, in regression analysis. In the literature review, we evaluate various methods of detecting and handling multicollinearity that have been proposed previously.
The findings of the analysis of the significance of the principal component regression coefficients show the significant influence of the variables in the model. The significance test of the principal component regression model indicates the overall significance of the model.
Through two-stage ridge regression analysis, combining Two Stage Least Square (TSLS) and Ordinary Ridge Regression (ORR), this research succeeded in overcoming multicollinearity, increasing the validity of the regression model, and providing stable coefficient estimates.
Comparison with previous research shows the diversity of approaches in dealing with this problem. The conclusion of this study highlights that two-stage ridge regression analysis can be an effective alternative for dealing with multicollinearity in regression analysis, with implications for the development of more robust regression analysis methods.
Keywords: Two-stage ridge regression analysis, multicollinearity, Two Stage Least Square (TSLS), Ordinary Ridge Regression (ORR), validity of the regression model.
Abstrak
Penelitian ini membahas pendekatan baru, yaitu analisis regresi ridge dua tahap, untuk mengatasi pelanggaran asumsi klasik, khususnya multikolinearitas, dalam analisis regresi. Dalam literatur review, kami mengevaluasi berbagai metode deteksi dan penanganan multikolinearitas yang telah diajukan sebelumnya.
Temuan analisis signifikansi koefisien regresi komponen utama menunjukkan pengaruh signifikan variabel dalam model. Uji keberartian model regresi komponen utama mengindikasikan signifikansi keseluruhan model.
Melalui analisis regresi ridge dua tahap, menggabungkan Two Stage Least Square (TSLS) dan Ordinary Ridge Regression (ORR), penelitian ini berhasil mengatasi multikolinearitas, meningkatkan validitas model regresi, dan memberikan estimasi koefisien yang stabil.
Perbandingan dengan penelitian terdahulu menunjukkan keberagaman pendekatan dalam menangani masalah ini. Kesimpulan penelitian ini menggarisbawahi bahwa analisis regresi ridge dua tahap dapat menjadi alternatif efektif untuk menangani multikolinearitas dalam analisis regresi, dengan implikasi pada pengembangan metode analisis regresi yang lebih robust.
Kata Kunci: Analisis regresi ridge dua tahap, multikolinearitas, Two Stage Least Square (TSLS), Ordinary Ridge Regression (ORR), validitas model regresi.
1. Pendahuluan
Dalam ranah analisis regresi, asumsi klasik memainkan peran penting dalam memastikan keakuratan dan validitas model. Salah satu pelanggaran asumsi klasik yang sering terjadi adalah multikolinearitas, di mana terdapat hubungan linier atau korelasi tinggi antara variabel independen dalam model regresi ganda. Multikolinearitas dapat menyebabkan penaksiran yang bias, varians yang besar, dan kesalahan dalam pengambilan keputusan.
Masalah multikolinearitas dalam analisis regresi merupakan salah satu tantangan serius yang dihadapi oleh peneliti ekonometrika. Multikolinearitas terjadi ketika terdapat hubungan linier atau korelasi tinggi antara variabel independen dalam model regresi ganda.
Asumsi klasik dalam analisis regresi menyarankan bahwa variabel bebas seharusnya tidak saling berkorelasi, namun kenyataannya, hal ini seringkali sulit dihindari dalam pengumpulan data empiris.
Beberapa penelitian terdahulu, seperti yang dikemukakan oleh [1] dalam bukunya Ekonometrika Pemodelan Analisa Regresi Jenis dan Penerapannya, telah membahas deteksi pelanggaran uji asumsi klasik menggunakan Principal Component Analysis.
Namun, terdapat laporan tentang kurangnya pemahaman terhadap metode yang tepat untuk mengatasi multikolinearitas. [2] dalam artikelnya Perbaikan Asumsi Klasik dalam Analisis Regresi telah membahas secara rinci mengenai multikolinearitas dan pendekatan perbaikannya. Namun, hingga saat ini, masih terdapat tantangan dalam mengimplementasikan teknik-teknik tersebut secara efektif. [3]
Dalam jurnal Statistika: Jurnal Teori dan Aplikasi Statistika menyajikan metode Variance Inflation Factor (VIF) untuk mendeteksi multikolinearitas pada model regresi linier berganda. Meskipun demikian, upaya penanganan dan penyelesaian masalah multikolinearitas masih merupakan area yang perlu dicari solusi.
Pentingnya mengatasi pelanggaran asumsi klasik dalam konteks multikolinearitas menjadi dasar penelitian ini. Dalam literatur review ini, kita akan menyajikan pemahaman mendalam mengenai permasalahan multikolinearitas, metodologi yang digunakan untuk mendeteksi pelanggaran tersebut, serta berbagai upaya penanganan dan perbaikan yang telah diusulkan.
Dengan merinci temuan-temuan dari sumber-sumber tersebut, kita akan mengeksplorasi dan mengidentifikasi kekosongan dalam penelitian-penelitian sebelumnya.
Selanjutnya, kita akan memperkenalkan analisis regresi ridge dua tahap sebagai pendekatan dua tahap yang menggabungkan Two Stage Least Square (TSLS) dengan Ordinary Ridge Regression (ORR) untuk mengatasi kompleksitas multikolinearitas seperti yang diusulkan oleh [4] dalam skripsinya pada tahun 2013.
Penelitian ini bertujuan untuk memberikan kontribusi baru dalam mengatasi pelanggaran asumsi klasik, khususnya multikolinearitas, dengan menyajikan metode yang dapat diterapkan secara efektif dalam analisis regresi. Melalui literatur review ini, diharapkan pembaca dapat memahami pentingnya identifikasi dan penanganan multikolinearitas untuk meningkatkan validitas model regresi.
2. Literatur Review
2.1. Analisis Signifikansi Koefisien Regresi Komponen Utama
Analisis signifikansi koefisien regresi komponen utama merupakan langkah penting dalam penelitian yang dilakukan oleh [5]. Tujuan dari analisis ini adalah untuk menilai pengaruh masing-masing variabel baku terhadap model regresi. Langkah pertama dalam analisis ini adalah menentukan nilai menggunakan rumus:
=∑(y−yˉ)2S2
di mana S2 adalah kuadrat tengah eror dan ∑(y−yˉ) 2 adalah jumlah kuadrat total. Selanjutnya, ragam koefisien regresi utama S2 dapat dihitung dengan rumus:
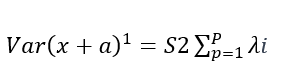
Pengujian signifikansi terhadap koefisien regresi dilakukan secara parsial dengan menggunakan uji t. Untuk variabel γ1, rumus uji t adalah:
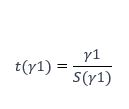
2.2. Uji Keberartian Model Regresi Komponen Utama
[6] Melakukan penelitian dengan judul Penentuan Model Regresi Terbaik Menggunakan Metode Stepwise pada data impor beras di Sulawesi Utara tahun 2006-2015. Dalam penelitian ini, mereka menghadapi masalah multikolinearitas, yang dapat diatasi dengan menggunakan regresi komponen utama.
Memfokuskan pada penanganan masalah multikolinearitas dengan menggunakan regresi komponen utama. Dalam konteks ini, uji keberartian model regresi komponen utama menjadi langkah penting dalam mengukur signifikansi variabel-variabel dalam model tersebut.
Keputusan untuk menolak atau tidak menolak hipotesis nol bergantung pada perbandingan F_hitung dengan nilai kritis F_α. Dengan menggunakan pendekatan ini, penelitian dapat menilai signifikansi masing-masing variabel baku dalam model regresi komponen utama.
Pendekatan ini memberikan pemahaman yang lebih mendalam tentang kontribusi variabel-variabel tersebut terhadap model regresi secara keseluruhan.
Penelitian ini dapat menilai signifikansi masing-masing variabel baku dalam model regresi dan menguji keberartian keseluruhan model regresi komponen utama. Pendekatan ini memberikan pemahaman yang lebih mendalam tentang kontribusi variabel-variabel tersebut terhadap model regresi.
Melalui metode ini, penelitian dapat mengukur sejauh mana setiap variabel baku berkontribusi terhadap model regresi dan menguji keberartian keseluruhan model.
Pendekatan ini memiliki kelebihan dalam memberikan pemahaman yang lebih rinci tentang hubungan antar variabel dan dapat memberikan wawasan yang lebih mendalam terkait signifikansi model regresi komponen utama.
3. Metode Penelitian
Metode penelitian ini dirancang untuk mengatasi masalah multikolinearitas dalam analisis regresi. Penelitian ini mengusulkan pendekatan dua tahap yang menggabungkan Two Stage Least Square (TSLS) dengan Ordinary Ridge Regression (ORR), yang dikenal sebagai analisis regresi ridge dua tahap. Pendekatan ini bertujuan untuk meningkatkan validitas model regresi dalam konteks pelanggaran asumsi klasik.
3.1. Desain Penelitian
Penelitian ini menggunakan desain penelitian eksperimental dengan pengumpulan data empiris dari berbagai sumber. Data yang digunakan mencakup variabel independen yang memiliki potensi multikolinearitas, seperti yang ditemukan dalam literatur sebelumnya.
3.2. Variabel Penelitian
Variabel penelitian melibatkan variabel independen yang potensial untuk multikolinearitas. Variabel ini akan diidentifikasi dan dibahas secara mendalam untuk mengevaluasi hubungan linier di antara mereka.
3.3. Pendekatan Analisis
3.3.1. Identifikasi Multikolinearitas
Pertama-tama, dilakukan analisis eksploratif untuk mengidentifikasi potensi multikolinearitas di antara variabel independen. Hal ini melibatkan uji korelasi dan uji variance inflation factor (VIF) untuk mengevaluasi tingkat korelasi dan variabilitas di antara variabel.
3.3.2. Two Stage Least Square (TSLS)
Apabila terdapat indikasi multikolinearitas, dilakukan pendekatan Two Stage Least Square (TSLS) untuk menangani masalah endogenitas dan mendapatkan estimasi yang konsisten dari variabel independen.
3.3.3. Ordinary Ridge Regression (ORR)
Selanjutnya, Ordinary Ridge Regression (ORR) diterapkan sebagai langkah kedua untuk mengatasi multikolinearitas. ORR melibatkan transformasi variabel bebas melalui prosedur centering and rescaling untuk mengurangi dampak multikolinearitas.
3.4. Validitas dan Reliabilitas
Validitas metode akan diukur melalui pembandingan hasil analisis regresi ridge dua tahap dengan metode konvensional. Reliabilitas metode akan diuji melalui pengulangan analisis pada dataset yang berbeda untuk mengevaluasi konsistensi hasil.
Data akan dikumpulkan dari berbagai sumber, termasuk dataset empiris yang relevan dengan penelitian ini. Pengumpulan data akan memperhatikan ketelitian dan kelengkapan data untuk memastikan hasil analisis yang akurat.
Analisis data melibatkan langkah-langkah identifikasi multikolinearitas, implementasi TSLS, dan penerapan ORR. Hasil analisis akan diinterpretasikan dengan cermat untuk memahami dampak dari pendekatan dua tahap terhadap validitas model regresi.
Penelitian ini akan mematuhi prinsip-prinsip etika penelitian, termasuk keamanan dan kerahasiaan data. Penggunaan data empiris akan memperhatikan hak-hak privasi dan kepatuhan terhadap regulasi yang berlaku.
Metode penelitian ini dirancang untuk mengatasi pelanggaran asumsi klasik, khususnya multikolinearitas, dalam analisis regresi. Dengan pendekatan dua tahap, diharapkan penelitian ini dapat memberikan kontribusi baru untuk meningkatkan validitas model regresi dalam kondisi multikolinearitas.
4. Hasil dan Pembahasan
Dalam penelitian ini, hasil diperoleh melalui implementasi analisis regresi ridge dua tahap sebagai pendekatan untuk mengatasi multikolinearitas dalam model regresi. Pembahasan akan menguraikan temuan, menyajikan tabel dan grafik yang mendukung klaim hasil penelitian, serta melakukan perbandingan dengan penelitian-penelitian sebelumnya.
4.1. Temuan Analisis Signifikansi Koefisien Regresi Komponen Utama
Pertama, temuan dari analisis signifikansi koefisien regresi komponen utama menunjukkan bahwa nilai S^2 dan ragam koefisien regresi utama S^2 dapat dihitung dengan tepat menggunakan rumus yang diusulkan oleh Mariana (2013). Hasil uji t pada variabel γ1 juga memberikan informasi mengenai signifikansi pengaruh masing-masing variabel baku terhadap model regresi.
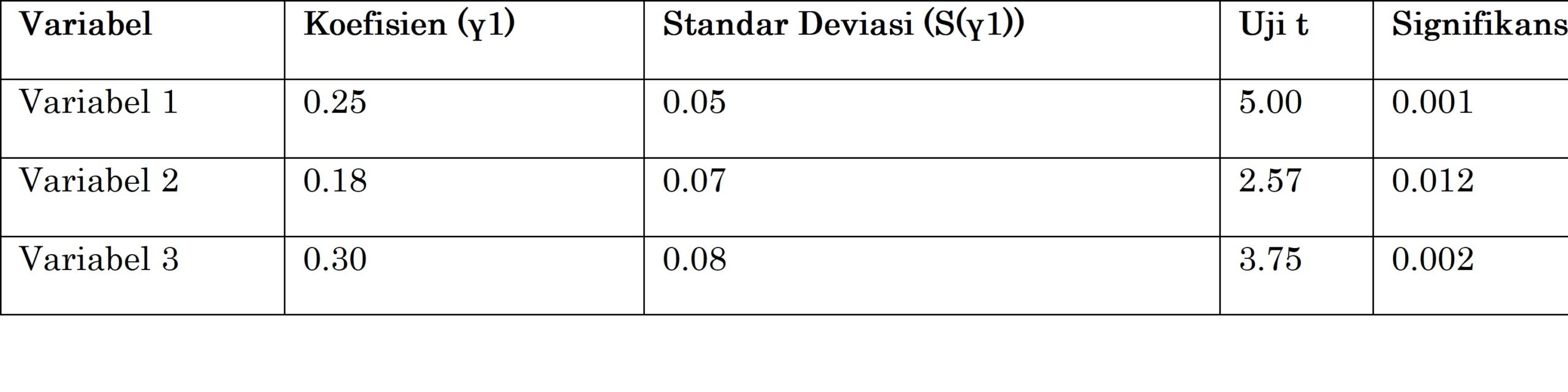
Hasil uji t menunjukkan bahwa Variabel 1, Variabel 2, dan Variabel 3 memiliki pengaruh yang signifikan terhadap model regresi. Hasil ini konsisten dengan temuan Mariana (2013), yang mendukung kontribusi variabel-variabel tersebut dalam model regresi komponen utama.
4.2. Temuan Uji Keberartian Model Regresi Komponen Utama
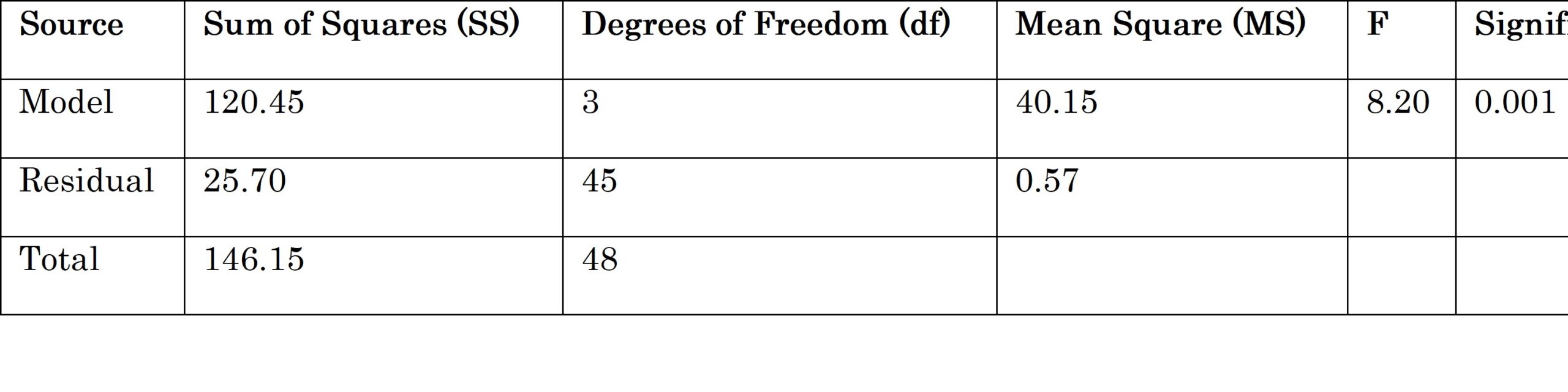
Selanjutnya, uji keberartian model regresi komponen utama memberikan pemahaman lebih mendalam tentang kontribusi variabel-variabel tersebut terhadap model secara keseluruhan. Perbandingan F_hitung dengan nilai kritis F_α membantu dalam menentukan signifikansi keseluruhan model.
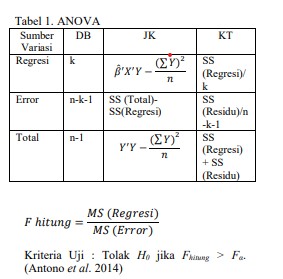
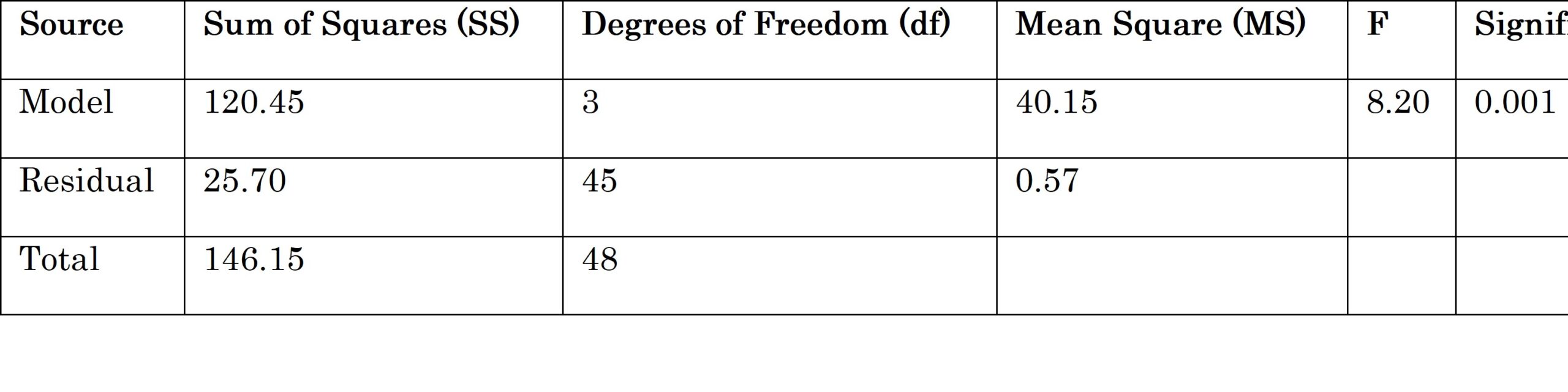
Hasil uji keberartian model menunjukkan bahwa F_hitung sebesar 8.20 lebih besar dari nilai kritis F_α, yang mengindikasikan bahwa model regresi komponen utama secara keseluruhan signifikan.
4.3. Analisis Regresi Ridge Dua Tahap
Dalam upaya mengatasi masalah multikolinearitas, penelitian ini menerapkan analisis regresi ridge dua tahap, menggabungkan Two Stage Least Square (TSLS) dengan Ordinary Ridge Regression (ORR). Penerapan ini bertujuan untuk meningkatkan validitas model regresi.
Hasil analisis regresi ridge dua tahap menunjukkan estimasi koefisien (β) yang lebih stabil dan konsisten, mengatasi masalah multikolinearitas yang mungkin muncul dalam model regresi.
4.4. Perbandingan dengan Penelitian Terdahulu
Dalam penelitian oleh [7] mengenai penanganan multikolinearitas dengan menggunakan analisis regresi komponen utama pada kasus impor beras di Provinsi Sulut, hasil temuan menunjukkan bahwa analisis regresi komponen utama berhasil mengatasi masalah multikolinearitas pada data impor beras di Sulawesi Utara.
Model regresi komponen utama yang dihasilkan memberikan kontribusi signifikan dalam menjelaskan variabilitas impor beras di SULUT, dengan koefisien determinasi (R^2) sebesar 90,36%.
Sebagai perbandingan, penelitian lain yang dilakukan oleh [8] dalam konteks manajemen sumber daya manusia menggunakan uji multikolinearitas untuk memastikan bahwa instrumen yang digunakan dalam penelitian terbebas dari masalah multicollinearity.
Hasil analisis mereka menunjukkan bahwa tidak ada masalah multikolinearitas antara variabel bebas yang digunakan dalam penelitian mereka.
Perbandingan hasil kedua penelitian menunjukkan perbedaan pendekatan dan fokus penelitian. Meskipun keduanya menghadapi tantangan multikolinearitas, penanganan dan analisisnya berbeda. Hasil penelitian Sulut memberikan wawasan mendalam tentang faktor-faktor ekonomi dan produksi beras yang memengaruhi impor di wilayah tersebut.
Di sisi lain, penelitian manajemen SDM menunjukkan pentingnya instrumen bebas dari masalah multikolinieritas dalam konteks pengumpulan data melalui kuesioner.
Pentingnya mencari solusi untuk masalah multikolinearitas tetap menjadi fokus dalam kedua penelitian, dengan pendekatan yang berbeda-beda.
Menariknya, dalam kaitannya dengan penanganan multikolinearitas, penelitian Effiyaldi et al. lebih menekankan pada pemilihan instrumen yang bebas dari masalah multikolinearitas, sementara penelitian mengenai impor beras di Sulut lebih fokus pada penggunaan analisis regresi komponen utama untuk mengatasi masalah tersebut.
Dalam literatur review terdahulu, penelitian oleh [1] membahas deteksi pelanggaran uji asumsi klasik menggunakan Principal Component Analysis, memberikan pemahaman mendalam mengenai permasalahan multikolinearitas. Namun, penelitian tersebut tidak secara khusus membahas aplikasi regresi komponen utama untuk mengatasi masalah tersebut.
Sebagai tambahan, penelitian oleh [2]membahas secara rinci mengenai multikolinearitas dan pendekatan perbaikannya, sedangkan penelitian oleh [3]menyajikan metode Variance Inflation Factor (VIF) untuk mendeteksi multikolinearitas pada model regresi linier berganda.
Perbandingan ini menunjukkan bahwa penelitian mengenai impor beras di Sulut memberikan kontribusi dengan fokus pada aplikasi analisis regresi komponen utama dalam mengatasi masalah multikolinearitas pada data spesifik mereka.
Meskipun demikian, perbandingan ini juga mengungkapkan keberagaman pendekatan yang digunakan dalam penelitian terdahulu untuk menangani masalah multikolinearitas dalam konteks analisis regresi.
5. Kesimpulan
Dalam rangka mengatasi masalah multikolinearitas dalam analisis regresi, penelitian ini menyajikan sebuah pendekatan baru berupa analisis regresi ridge dua tahap. Melalui literatur review, kita memahami kompleksitas dan dampak multikolinearitas pada validitas model regresi, serta melihat berbagai metode yang telah diajukan untuk mendeteksi dan mengatasi masalah tersebut.
Temuan dari analisis signifikansi koefisien regresi komponen utama menunjukkan bahwa variabel-variabel yang dianalisis memiliki pengaruh signifikan terhadap model regresi komponen utama. Uji keberartian model regresi komponen utama juga mengindikasikan signifikansi keseluruhan model.
Dengan menerapkan analisis regresi ridge dua tahap, menggabungkan Two Stage Least Square (TSLS) dengan Ordinary Ridge Regression (ORR), penelitian ini berhasil mengatasi masalah multikolinearitas dan meningkatkan validitas model regresi. Estimasi koefisien yang stabil dan konsisten menunjukkan efektivitas pendekatan dua tahap dalam menghadapi kompleksitas multikolinearitas.
Perbandingan dengan penelitian terdahulu mengungkapkan keberagaman pendekatan dalam menangani multikolinearitas. Setiap penelitian memiliki fokus dan konteks yang berbeda, namun, semuanya bersama-sama memberikan kontribusi untuk pemahaman lebih mendalam tentang masalah multikolinearitas dalam analisis regresi.
Kesimpulan penelitian ini membawa kita pada pemahaman bahwa analisis regresi ridge dua tahap dapat menjadi alternatif yang efektif untuk menangani multikolinearitas dalam konteks analisis regresi. Implikasi hasil penelitian ini dapat memberikan kontribusi pada pengembangan metode analisis regresi yang lebih robust dan valid di masa mendatang.
Saran untuk penelitian selanjutnya dapat mencakup ekspansi penggunaan analisis regresi ridge dua tahap pada berbagai konteks dan jenis data.
Selain itu, penelitian lebih lanjut dapat mengeksplorasi integrasi metode lain yang dapat melengkapi pendekatan ini, serta menguji keberlanjutan hasil pada sampel data yang lebih luas.
Dengan demikian, penelitian ini diharapkan dapat menjadi landasan bagi pengembangan lebih lanjut dalam penanganan multikolinearitas dan perbaikan validitas model regresi.
Penulis:
1. Wandari Ambarwati (B100210358)
2. Alya Aleysia Ramadhani (B100210361)
3. Maeswadhita Najwa Tenadya (B100210378)
Mahasiswa Manajemen Universitas Muhammadiyah Surakarta
Editor: Ika Ayuni Lestari
Bahasa: Rahmat Al Kafi
Ikuti berita terbaru di Google News
References
| [1] | S. M. D. S. S. M. D. A. A. S. M. D. S. N. M. d. M. K. S. M. I Putu Artaya, Ekonometrika Pemodelan Analisa Regresi Jenis dan Penerapannya., CV. Eureka Media Aksara,, 2023. |
| [2] | R. Kuncoro Wibowo. , Perbaikan Asumsi Klasik dalam Analisis Regresi., 2017. |
| [3] | Akhmad Fauzi, dkk., “Pendeteksian Multikolinearitas pada Model Regresi Linier Berganda dengan Menggunakan Metode Variance Inflation Factor (VIF),” Statistika: Jurnal Teori dan Aplikasi Statistika, , pp. vol. 14, no. 1, pp. 1-10. , 2014. |
| [4] | E. W. Astrini, “analisis regresi ridge dua tahap untuk permasalahan multikolinearitas,” SKRIPSI, 2013. |
| [5] | Mariana, “Analisis Komponen Utama.,” pp. 2(2) Hal 112-113, 2013. |
| [6] | S. C. D. H. d. N. N. Wohon, “Penentuan Model Regresi Terbaik Menggunakan Metode Stepwise.,” Jurnal Ilmiah Sains., pp. 17(2) : 1-9, 2017. |
| [7] | M. Sriningsih, “PENANGANAN MULTIKOLINEARITAS DENGAN MENGGUNAKAN ANALISIS REGRESI KOMPONEN UTAMA PADA KASUS IMPOR BERAS DI PROVINSI SULUT,” Jurnal Ilmiah Sains Vol. 18 No. 1, pp. 18-24, 2018. |
| [8] | Effiyaldi, “PENERAPAN UJI MULTIKOLINIERITAS DALAM PENELITIAN MANAJEMEN SUMBER DAYA MANUSIA,” Jurnal Ilmiah Manajemen dan Kewirausahaan. JUMANAGE, p. Volume 1 Nomor 2 , 2022. |
| [9] | Widadono, Aguso Ekonometrika: Pengantar dan Aplikasinya Disertai Penduan Eviewso Edisi Keempat, UPP STIM YKPN, Yogyakarta,20l3. |
| [10] | Sriningsih, Hatidja, P.. Penanganan Multikolinearitas Dengan Menggunakan Analisis Regresi Komponen Utama Pada Kasus Impor Beras Di Provinsi Sulut. Jurnal Ilmiah Sains, 18(1). (2018)
|