Analisis Jumlah Kasus Positif Covid-19 Bulan Agustus

Teori forecasting (peramalan) dalam statistika memiliki 3 metode peramalan statistika sederhana, yaitu :

1. Metode Semi Rata-Rata (Semi Average Method)
2. Metode Trend Moment
3. Metode Kuadrat Terkecil (Least Square Method)

Dalam analisis jumlah kasus positif covid-19 penulis akan menggunakan metode Semi Rata-Rata (Semi Average Method)dan penulis akan menggunakan data kasus positif covid-19 dibawah ini:

Bulan	Jumlah Pasien Positif Covid-19
Maret	1.528 orang
April	10.118 orang
Mei	26.473 orang
Juni	56.385 orang
Juli	108.376 orang
Jumlah	202.880 orang

Metode Semi Rata-Rata

Jumlah seluruh data di atas adalah 5 data (Ganjil ). Oleh karena itu analisis data dilakukan dengan cara sebagai berikut:

• Mengelompokkan data menjadi 2 kelompok. Dengan cara, Memisalkan penduplikasiaan data yang terletak di tengah yaitu data Bulan Mei, Sehingga Kelompok 1 : Maret, April, Mei dan Kelompok 2 : Mei’ , Juni, Juli
• Menentukan  periode dasar. Misalnya diasumsikan periode dasar menggunakan tahun tengah data tahun kelompok 1, sehingga periode dasarnya adalah Bulan April
• Menentukan Angka Tahun. Karena periode dasar Bulan April maka angka tahun x = 0, maka angka tahun untuk bulan Maret adalah -1 dan angka tahun untuk Mei, Juni, Juli, Agustus berturut-turut adalah 1, 2, 3, 4 dst.
• Menentukan nilai Semi Total yakni Jumlah total Kasus Covid-19. Untuk kelompok 1 : Nilai Semi Totalnya adalah 1528 + 10118 + 26473 = 38119. Nilai Semi Total Kelompok 2 yaitu 26473 + 56385 +108376 = 191234
• Menentukan Semi Average tiap kelompok data. Semi Average untuk kelompok 1 adalah (semi total kelompok 1 dibagi jumlah data kelompok 1 sehingga nilainya adalah 38119/3 = 12706,33. Semi Average untuk Kelompok 2 yaitu 191234/3 = 63744,67

Ringkasan Perhitungan Jumlah Kasus Positif Covid-19

Ringkasan Perhitungan disajikan pada tabel berikut:

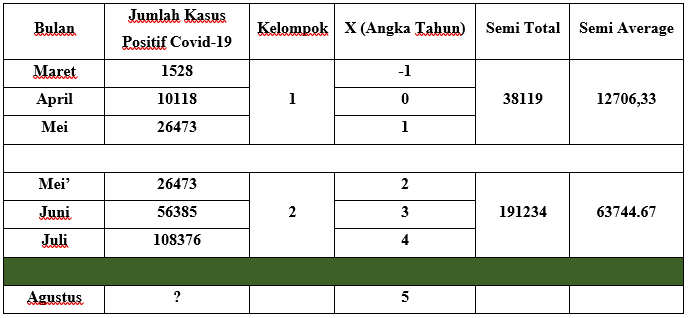
Dari perhitungan tersebut di atas, ditentukanlah nilai a dan b sehingga diperoleh fungsi persamaan untuk peramalan dengan cara sebagai berikut :

• Nilai a ditentukan berdasarkan nilai Semi Average untuk kelompok yang tahun tengahnya digunakan sebagai periode dasar. Pada kasus ini periode dasar menggunakan tahun tengah kelompok 1, sehingga nilai a adalah sebesar nilai Semi Average kelompok 1 yakni 12706,33
• Menentukan nilai b.  Karena Jumlah data dalam kelompok adalah ganjil maka untuk menentukan nilai b dapat langsung dengan cara membagi selisih antara nilai Semi Average kelompok 2 dan 1 dengan jumlah data dalam kelompok sehingga hasilnya (63744,67 – 12706,33) / 3 = 17012,78
• Menentukan Fungsi Peramalan. Karena nilai a = 12706,33 dan nilai b = 17012,78 maka fungsi peramalannya adalah Y = 12706,33 + 17012,78X

Penjabaran Perhitungan Jumlah Kasus Positif Covid-19

Perhitungan selengkapnya adalah sebagai berikut:

a = 12706,33

b =  

Fungsi Peramalan :     Y = a + bx

                                    Y = 12706,33 + 17012,78X

Dengan menggunakan fungsi peramalan yang diperoleh dengan metode Semi Average tersebut selanjutnya dilakukan prediksi jumlah kasus covid-19 pada bulan Agustus dimana angka tahun bulan Agustus adalah 5 atau (X = 5). Prediksi Jumlah Kasus Covid-19 pada Bulan Agustus di Indonesia adalah 110477

Agustus :

 x = 5

Y = 12706,33 + 17012,78X

Y = 12706,33 + 17012,78 (5)

Y = 12706,33 + 97770,23

Y = 110476,56

Y 110477

Jika hasil ini tidak akurat , maka penulis akan melakukan analisis lanjutan dengan membandingkan dua metode lainnya. Terimakasih

Note : Tidak semua metode dapat dilakukan di semua data. Dibutuhkan analisi MSE, MAPE, MFE atau MAD untuk menganalisa keakuratan metode terhadap data tersebut.

Refrensi : Vincent Gaspersz : Statistical Process Control, 1998

Mutiah Nasution
Mahasiswa Universitas Islam Negeri Sumatera Utara (UINSU)

Editor: Muhammad Fauzan Alimuddin

Baca Juga:
Peran Media di Tengah Wabah Covid-19
Covid-19 Masih Mengancam, DPC GMNI Jepara : Pembelajaran Tatap Muka Masih Riskan
Covid-19 Belum Tuntas, Kenapa Bahas RUU HIP?